|
Dynamika symboliczna i kody
Geneza Układy
dynamiczne pojawiły się na początku XVIII w wraz z pojawieniem się
dynamiki newtonowskiej. Ruch planet odbywa się zgodnie z zasadami
opisanymi przez układ równań różniczkowych. Przez cały wiek XVIII i
XIX matematycy tacy jak Euler czy Jacobi rozwijają metody rozwiązywania
równań różniczkowych w celu znalezienia jawnych rozwiązań równań
ruchu. W tym czasie powstała analiza zespolona, analiza fourierowska.
Mimo pojawienia się tak potężnych narzędzi jawne równania ruchu udaje
się znaleźć tylko w niewielu szczególnych przypadkach. Pod koniec XIX
w. pojawiają się pierwsze twierdzenia z abstrakcyjnej teorii
ergodycznej: twierdzenie Poincaré,
twierdzenie ergodyczne. Jednak wyniki te odnoszone są wciąż do gładkich
układów dynamicznych. Przeglądając
Journal de Mathématiques
z 1898 r. znajdujemy prace Poincaré,
Laurenta, Lapunowa, Jordana. W większości dotyczą one równań różniczkowych,
lub gładkich układów dynamicznych. Jest tam też praca Hadamarda dotycząca
krzywych geodezyjnych na powierzchniach o ujemnej krzywiźnie. Ta właśnie
praca odegrała ogromną rolę w powstaniu dynamiki symbolicznej. Hadamard
rozpatruje homotopijne klasy krzywych. Wykazuje on, że istnieje skończony
układ krzywych G={g1,
g2, ... ,gn}, taki że każda klasa homotopii odpowiada
wielokrotnemu obieganiu krzywych z tego układu w określonej kolejności,
a więc opisuje się ciągiem A
= ... a-1, a0,
a1,...
(ai
ÎG).
Następnie dowodzi on, że każda taka klasa zawiera dokładnie jedną
geodezyjną. Przy dodatkowym założeniu, że rozmaitość ta poza pewnym
obszarem ograniczonym składa się ze skończonej liczby rozszerzających
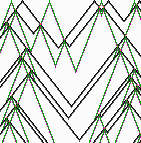
się „rękawów”, otrzymamy tak wszystkie geodezyjne ograniczone. Na
rysunku widzimy przykład takiej rozmaitości. Nietrudno zauważyć, że
geodezyjna, jeśli ma być ograniczona, musi przechodzić przez „siodła”
pomiędzy „rękawami”. Ponieważ są trzy „siodła”, więc na każdym
z nich może ona skręcać w kierunku jednego z pozostałych dwóch siodeł.
Dzięki temu geodezyjna taka daje się zakodować ciągiem o dwóch
symbolach. Istotnie, w metodzie Hadamarda dla tej rozmaitości G jest
zbiorem dwuelementowym.
Pomysł
Hadamarda wykorzystał w latach 1920-21 amerykański matematyk Harold
Marston Morse. W owych czasach znane już było pojęcie układu
minimalnego, oraz kryterium jednostajnego powracania. Potrzebny był przykład
takiego układu, który nie byłby okresowy. Po pierwsze Morse wykazał,
że kodowanie Hadamarda jest ciągłe w tym sensie, że jeśli dwa ciągi
zgadzają się na długim bloku, to odpowiadające im geodezyjne przez długi
czas przebiegają blisko siebie. Po drugie wykazał on, że ciągom
okresowym odpowiadają dokładnie geodezyjne zamknięte. Współcześnie mówiąc
sprowadził on badanie potoku geodezyjnego do badania układu
symbolicznego
(GZ,S)
. Następnie podał on przykład ciągu nad alfabetem dwuelementowym, o
żądanych własnościach (jednostajnie powracający i nieokresowy). Ciąg
ten współcześnie znany jest jako ciąg Morse’a. Powstaje one przez „negowanie” już powstałych
bloków: 0-1-10
-1001-10010110-1001011010011001-... Istotny
jest skok jakościowy jakiego dokonał Morse. Stworzył on narzędzie całkowicie
niezależne od stosowanych do tego czasu gładkich układów dynamicznych.
Dlatego to właśnie Morse’a należy uważać za ojca współczesnej
dynamiki symbolicznej. Jest cechą charakterystyczną wielkich odkryć, że
ich autorzy często nie dostrzegają wagi swoich dokonań polegających na
stworzeniu zalążków nowej teorii. Morse nadal formułuje wszystkie
twierdzenia i wnioski w języku potoków geodezyjnych na powierzchniach o
ujemnej krzywiźnie. Jednak już w roku 1938, wraz z Gustawem
Arnoldem Hedlundem pisze on pracę pt. „Symbolic Dynamics” w całości
poświęconą badaniu abstrakcyjnych układów symbolicznych. (Niektórzy
matematycy polscy stosują tłumaczenie „dynamika symbolowa”, zapewne
dlatego, że słowo „symboliczna” ma w języku polskim określone
zabarwienie znaczeniowe - określa coś posiadającego niewielką wartość
materialną, jak np. w zwrotach „symboliczny prezent” albo
„symboliczna płaca”). W
książce „Topological Dynamics” Gottshalka-Hedlunda z 1955 r.
dynamika symboliczna zajmuje osobny rozdział. Wiadomo, że układy
symboliczne opisują dokładnie te układy topologiczne, które spełniają
dwa warunki: zero-wymiarowość i ekspansywność.
Zastosowania Rozważmy
gładki układ dynamiczny. Ponieważ nie sposób jest analizować danych w
postaci dokładnych współrzędnych wszystkich punków we wszystkich chwilach
czasu, przeprowadza się tak zwaną redukcję danych. Dzieli się w tym celu
zbiór na skończenie wiele części oznaczonych symbolami (w
odwzorowaniach odcinka najczęściej są to lewa i
prawa strona: L i R). Dla każdego
punktu zapisuje się do której z tych części wpada on przy
kolejnych iteracjach. Otrzymujemy w ten sposób nieskończony ciąg skończenie
wielu liter (symboli), np. LRRLLLRLRRLLLRRLRRRRLRLLRL...
W
przypadku odwzorownia odcinka z jednym maximum ciąg utworzony tak dla punktu
krytycznego nazywany jest wygniotkiem.
W ogólnym przypadku mówimy o faktorze generowanym przez dany podział.
Wbrew pozorom, przejście to nie wiąże się ze stratą dużej ilości
danych. Teoretycznie można dowieść, że w wielu przypadkach, przy
odpowiednio dobranym podziale zbioru uzyskany układ
symboliczny jest izomorficzny (a więc zawiera pełną informację) z układem
wyjściowym. Badaniem właśnie takich ciągów zajmuje się dynamika
symboliczna. W przypadku prostych transformacji (odbicie symetryczne)
otrzymamy ciąg okresowy, np. LRLRLRLR... , a w skrajnie skomplikowanym - ciąg
wyglądający jak ciąg losowy, tzn. taki jaki otrzymalibyśmy w wyniku
kolejnych rzutów monetą: LLRLRRLRRLLLRLRLLRRRLRRLL...
. Ciąg
taki ma na przykład tę własność, że przy ustalonym n
każdy blok długości n występuje
w nim jednakowo często (np. LL pojawia się równie często jak LR czy RR, a
LLLLLL jak RRRRRR oraz jak na przykład LRLRLR, itp.). Pomiędzy ciągami
okresowymi i pseudolosowymi istnieje oczywiście cała gama możliwości pośrednich.
Dochodzimy tu do niezwykle ważnego odkrycia: otóż proces, który
obserwujemy jest w pełni deterministyczny (tzn. pozbawiony losowości - znając
transformację i współrzędne punktu wyjściowego można dokładnie wyliczyć
współrzędne jego obrazu), a jednak można uzyskiwać wygniotek o cechach ciągu
losowego. Stopień podobieństwa
do procesu losowego mierzy tzw. entropia
układu. Istnieje wiele różnych definicji entropii w układach dynamicznych.
Entropia układu symbolicznego jest zdefiniowana właśnie w terminach częstości
występowania różnych bloków tej samej długości. Mała entropia oznacza
dominację niewielkiej grupy bloków w całym ciągu. Z entropią wiąże się
bezpośrednio pojęcie chaosu. Nieco
upraszczając można powiedzieć, że chaos to niezerowa entropia. Zatem układy
dynamiczne dzielą na układy chaotyczne i te pozbawione zupełnie pozorów
losowości (np. okresowe, ale nie
tylko).
Kody blokowe Wyobraźmy
sobie, że naszą przestrzeń podzieloną na części L i R dzielimy też w
inny sposób na A i B. Przy ustalonym punkcie początkowym otrzymamy teraz
dwie jego reprezentacje, np. x =
LRRLLLRLRRLLLRRLRRRRLRLLRLL... oraz y = BAABABBAAABABAAAAAAAABBBBB... Obydwa
te ciągi opisują trajektorię tego samego punktu w tym samym układzie
dynamicznym. Zachodzi więc pytanie, czy między tymi ciągami istnieje jakiś
kombinatoryczny związek. Okazuje się, że tak. Otóż przy pewnych założeniach
istnieje między nimi tzw. kod blokowy,
czyli istnieje słowniczek pomiędzy wszystkimi blokami pewnej ustalonej długości
no (czasem bardzo dużej) liter L i R, a pojedynczymi
symbolami A i B, taki że pod środkiem każdego bloku długości no
w x widzimy w y
literę A lub B według tego słowniczka. W naszym przykładzie no
= 3 a
kod blokowy jest następujący: LLL
>> A LLR
>> B LRL
>> B LRR
>> A RLL
>> B RLR
>> A RRL
>> A RRR
>> A lub
zastępując w obu ciągach symbole przez 0 i 1 000
>> 0 001
>> 1 010
>> 1 011
>> 0 100
>> 1 101
>> 0 110
>> 0 111
>> 0 Kody blokowe badane były jako obiekt abstrakcyjny mniej więcej od połowy stulecia. Odkryto wiele fascynujących własności tych niezwykle prostych przekształceń. Do najważniejszych należą wyniki Hedlunda z końca lat 60-tych. Kody blokowe odgrywają ważną role w teorii układów dynamicznych, gdyż przy ich pomocy opisuje się znaczna część morfizmów pomiędzy układami dynamicznymi. Ponadto kod blokowy (jeśli używamy tu i tu tych samych symboli) można również iterować, przez co również generuje on układ dynamiczny (działający na zbiorze ciągów) zwany automatem.
Zastosowania kodów Kody blokowe znalazły niedawno szerokie zastosowania w
informatyce i teorii informacji. Wyobraźmy
sobie
prymitywny czarno-biały obrazek komputerowy, tzw. bitmapę. Ponieważ jest
czarno-biała, można ją zapisać w formie ciągu zer i jedynek (0 - piksel
biały, 1 - piksel czarny). W zasadzie każdy plik komputerowy wygląda właśnie
w ten sposób. Wprowadźmy podział tego ciągu na bloki czwórkowe. Istnieje
16 możliwych takich bloków 0000, 0001, i wszystkie najprawdopodobniej występują w naszym pliku. Będziemy próbowali zastępować je w sposób odwracalny blokami krótszymi. Dwa z nich można zastąpić blokami długości 1, cztery - blokami długości 2, osiem - długości 3 i tylko dwa zostaną tej samej długości. 0000
>> 0 1111
>> 1 0011
>> 00 1100
>> 11 0101
>> 01 1010
>> 10 0110
>> 000 1001
>> 001 0001
>> 010 1110
>> 011 0111
>> 100 1000
>> 101 0100
>> 110 1011
>> 111 0010
>> 0000 1101
>> 0001 Jest to nieco inny rodzaj kodu niż omawiany do tej pory, gdyż obrazami są nie pojedyncze symbole lecz bloki o różnych długościach, ale nie jest to bardzo istotna różnica. Przekodujmy teraz naszą bitmapę. W większości przypadków uzyskamy kompresję mniej więcej 60%-ową. Większość z nas na co dzień stosuje różne programy kompresujące, być może nie zdając sobie sprawy, że są to właśnie kody blokowe. Oto dwie większe bitmapy czarno-białe o tych samych rozmiarach i tej samej rozdzielczości.
W
efekcie są to pliki tej samej wielkości i zajmują tyle samo miejsca na
dysku. Co więcej, zadbano nawet o to, żeby miały one jednakową proporcję
piksli czarnych do białych. Użyjmy teraz do ich kompresji jakiegokolwiek
standardowego programu typu ZIP. Co się okaże? Jedna z bitmap ulegnie
kompresji w stopniu prawie 5 razy większym niż druga. Dlaczego? Odpowiedź
tkwi w entropii. Im większa entropia, tym gorsza kompresja. Program kompresujący
sprawdza najpierw które z bloków danej długości kodowania występują
najczęściej i te bloki kodowane są w pierwszej kolejności - blokami krótkimi.
Jeśli entropia jest duża, to zabieg ten ma niewielkie znaczenie, gdyż
wszystkie bloki występują podobnie często. Przy małej entropii jednak można
dzięki temu zabiegowi dodatkowo zaoszczędzić dużo miejsca.
Automaty komórkowe Kod, podobnie jak każdą inną transformację, można wielokrotnie iterować. I znowu możemy, w zależności od kodu i ciągu wyjściowego otrzymywać różne „ciągi ciągów” o rozmaitych cechach od okresowych do całkowicie chaotycznych. Powróćmy do naszego pierwszego przykładu kodu i prześledźmy kolejne obrazy ciągu zawierającego same zera i jedną jedynkę. Oto co zobaczymy:
Piksle czarne to jedynki, białe to zera. To co widzimy przypomina tak zwany trójkąt Sierpińskiego. Jest to podzbiór płaszczyzny dobrze znany matematykom, powstały przez powtarzanie nieskończenie wiele razy czynności polegającej na usuwaniu mniejszych trójkątów ze środków trójkątów większych. Tutaj otrzymaliśmy trójkąt Sierpińskiego zupełnie inną metodą. Obrazek ten ma tę własność, że jego mały fragment oglądany w powiększeniu przypomina całość. Własność ta nosi nazwę samopodobieństwa. Zbiór ten to samopodobny fraktal. Fraktale pojawiają się w wielu działach teorii układów dynamicznych, gdyż powstają one właśnie w wyniku wielokrotnego powtarzania tej samej operacji. Odkrycie fraktali stało się możliwe dzięki wprowadzeniu techniki komputerowej, gdyż przy pomocy tablicy i kredy nie jest możliwe symulowanie kilkuset iteracji. Potrzebna też jest wysoka rozdzielczość obrazu. Jednak to nie człowiek wymyślił fraktale. Występują one od dawna w przyrodzie. To zdjęcie przedstawia kalafior stożkowy: jego fragment przypomina całość.
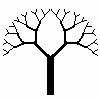
Fraktali
można dopatrzyć się w wielu roślinach i to zarówno w skali makro- (paproć,
drzewo), jak i mikroskopowej (żyłkowanie liścia). Oznacza to, że w trakcie
wzrostu rośliny mamy do czynienia z wielokrotnym powtarzaniem tego samego
schematu. Na przykład, jeśli gałąź ma zakodowaną tendencję do
podzielenia się na dwie i te cechę przekazuje każdej z nich, to w efekcie
otrzymamy strukturę dychotomiczną tak charakterystyczną dla wielu roślin.
Automaty komórkowe występujące w przyrodzie I tak oto wkroczyliśmy na tereny nauk przyrodniczych. Przyroda fascynowała ludzi od wieków. Fascynowała swym pięknem i bogactwem form. Któż nie zachwycał się kolorowymi wzorami i deseniami jakimi mogą poszczycić się niektóre ryby, motyle lub inne żyjątka. Projekt każdego ornamentu jest charakterystyczny dla danego gatunku i przechowywany w kodzie genetycznym, dzięki czemu może on być przekazywany z pokolenia na pokolenie. W miarę rozwoju organizmu, dzielące się komórki przyjmują kształt, funkcję i kolor zgodnie z rozkazem zawartym w odpowiednim fragmencie nici DNA. Sposób w jaki realizowany jest zapis genetyczny jest przedmiotem badań genetyków i mikrobiologów.
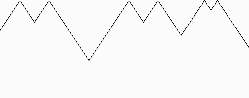
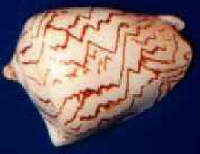
Wśród tych zdjęć jedno jest jednak wyjątkowe i przedstawia zjawisko, które przez wiele lat stanowiło dla biologów nie lada zagadkę. Chodzi tu o muszle ślimaków. Skorupa jest bowiem całkowicie martwa, a nawet pozbawiona struktury komórkowej i nie może tu być mowy o genetycznym zakodowaniu ornamentu. Skorupa powstaje w wyniku ciągłego odkładania się wapnia na jednej z krawędzi. Krawędź ta styka się z płaszczem ślimaka, gdzie stale odkładany jest wapń. W miejscu tym znajdują się komórki pigmentowe ułożone w jeden rząd, których zadaniem jest dodawanie do wapna odpowiednich barwników. Komórki pigmentowe ustawicznie zmieniają swój stan włączając lub wyłączając swą produkcję. W tym sensie ślimak przypomina nieco drukarkę wierszową, a skorupa - wydruk rejestrujący na wysuwającym się papierze zmieniający się stan nieruchomej „głowicy”. Instrukcja o zmianie stanu poszczególnych komórek nie może pochodzić z kodu genetycznego, gdyż zmiany te nie są związane z podziałem i reprodukcją samych komórek. Jeśli chodzi o stymulację przy pomocy sygnałów hormonalnych, to ustalono na podstawie badań, że rozchodzą się one równomiernie w ciele ślimaka i mogą co najwyżej powodować powstawanie na skorupie poziomych pasów, tak jak to widać na tych przykładach.
Wobec tego jak powstają wszystkie inne, o wiele bardziej złożone ornamenty na muszlach? Mechanizm powstawania bardziej skomplikowanych wzorów wyjaśnił na początku lat 50-tych Alan Turing posługując się dyfuzją międzykomórkową. Każda komórka, oprócz pigmentu może produkować jeszcze co najmniej dwie substancje: tzw. aktywator i inhibitor. Mała ilość aktywatora prowokuje komórkę do produkcji aktywatora, przy większym stężeniu - pigmentu, a przy jeszcze większym - inhibitora. Inhibitor rozkłada aktywator, i po pewnym czasie sam zanika. Dodatkowo, aktywator może przenikać przez ściany komórkowe do komórek sąsiednich. Pobudzenie danej komórki zostało zamodelowane układem równań różniczkowych zależnych od pobudzenia komórek sąsiednich. Rozwiązanie takiego układu równań możliwe jest tylko metodami przybliżonymi. Chociaż model taki daje ostatecznie dużą zgodność z rzeczywistością, to jest on jednak bardzo skomplikowany i pozwalał się stosować tylko do niektórych deseni. W roku 1990 Przemysław Prusinkiewicz zauważył podobieństwo ornamentów na niektórych muszlach do obrazów uzyskanych komputerowo przy pomocy kodów blokowych o długości kodowania 3. Oto porównanie jednej z muszli i obrazu uzyskanego przy pomocy tego samego kodu co trójkąt Sierpińskiego, ale przy linii początkowej zawierającej kilkanaście nieregularnie umieszczonych jedynek.
Podobieństwo
to sugeruje, że komórki pigmentowe realizują podobny kod. Trzeba dokonać
tzw. dyskretyzacji czasu, to znaczy podzielić go na jednostki (odpowiednie do
czasu płynącego w „ślimaczym tempie”; za jednostkę przyjmiemy czas
potrzebny na przyrost muszli powiedzmy o jeden milimetr). Wtedy stan danej komórki
w danej chwili zależeć będzie od stanu tej i dwóch sąsiednich komórek w
chwili poprzedniej. Oddziaływanie opisane przez Turinga można wstępnie
zamodelować kodem o trzech symbolach: 0, 1, 2 (nic, aktywator, inhibitor) w
następujący sposób: *,
1, * >>
2 1,
0, * >>
1 *,
0, 1 >>
1 *,
2, * >>
0 reszta
>>
0 Dokonując symulacji takiego kodu przy kilku nieregularnie rozmieszczonych aktywnych komórkach otrzymujemy taki oto obraz:
Jak widać, linie rozchodzą się pod pewnym kątem, a przy spotkaniu zanikają. Podobne linie występują u kilku gatunków ślimaków, jednakże oprócz zanikania potrafią one także nieoczekiwanie dzielić się.
Stanie się tak jeśli z jakiegoś powodu inhibitor w komórce zaniknie szybciej, co pozwoli komórce „zarazić się” aktywatorem od komórki przed chwilą przez nią samą uaktywnioną. Początkowo przy wyjaśnianiu tego zjawiska użyto argumentu losowego, to znaczy założono, że coś takiego zdarza się spontanicznie od czasu do czasu. Wyjaśnienie to jednak nie jest satysfakcjonujące. Wiemy, że pozory losowości nie wykluczają czysto deterministycznego wyjaśnienia. Potrzebna jest do tego niezerowa entropia. Wyobraźmy sobie, że komórki pigmentowe produkują jeszcze dwie inne substancje, które doprowadzają do powstawania podobnych lecz nie uwidaczniających się na skorupie linii ukośnych biegnących po innym kątem. W miejscu spotkania obu rodzajów linii powstaje mniej inhibitora (obu rodzajów) i obie linie dzielą się. Oto obraz uzyskany przy pomocy kodu o ośmiu symbolach, który realizuje takie założenia (aż 8, bowiem trzeba teraz uwzględnić różne stężenia czterech substancji).
Widzimy tu oba rodzaje linii i ich rozdwajanie się. Ponieważ drugi rodzaj linii nie uwidacznia się na powierzchni skorupy, możemy użyć w odpowiednich stanach koloru białego, wtedy zobaczymy obraz dość zbliżony do rzeczywistych wzorów na muszli ślimaka z gatunku Olivia porphyria.
Można
teraz zastanawiać się jaka jest praktyczna wartość tego naukowego
odkrycia. Na temat wzorów na muszlach napisano dwie książki oraz kilka artykułów
naukowych i popularno-naukowych. Wzajemne oddziaływanie komórek występuje
prawdopodobnie w każdej tkance. Problem polega na tym, że rzadko komórki te
ułożone są w jeden rząd, a w strukturach przestrzennych odpowiednie kody
stają się niezwykle skomplikowane. Kombinatoryczna teoria takich kodów jest
dopiero w powijakach. Jednak rozwój tej teorii może w przyszłości pomóc w
lepszym rozumieniu wielu zjawisk zachodzących w organizmach żywych. Kody blokowe wymyślono i badano jako obiekt czysto abstrakcyjny. Następnie znalazły one wiele praktycznych zastosowań w teorii informacji, w końcu okazało się, że modelują one zjawiska występujące w przyrodzie od zarania dziejów, i że wyniki teoretycznych badań mogą przyczynić się do lepszego poznania świata ożywionego. Myślę, że jest to doskonały przykład wyjaśniający, dlaczego nauki abstrakcyjne nie są, jak się często uważa, tylko sztuką dla sztuki. Przyrodą i matematyką rządzą te same prawa, pytanie tylko, na ile naukowcy z tych odległych dziedzin potrafią wykorzystać wzajemnie swoje osiągnięcia. |