Zadanie 8
Na rysunku przedstawiono wykres funkcji
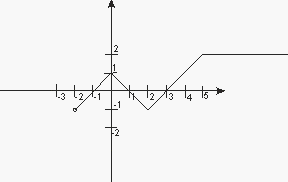
Dziedziną funkcji jest
A
B
C
D
Odczytujemy dziedzinę z rysunku. Widzimy, że funkcja jest określona dla wszystkich spełniających warunek
Prawidłowa odpowiedź to odpowiedź C.
Kliknij w numer wybranego zadania, jeśli chcesz je zaznaczyć jako przerobione.
Możesz dowolnie zaznaczać zadania i usuwać zaznaczenia.
Jednak Twoje zaznaczenia nie będą widoczne po odświeżeniu strony.
Zadanie 1
Największą liczbą spełniającą nierównosć jest
Przekształcamy podaną nierówność:
Prawidłowa odpowiedź to odpowiedź A.
Zadanie 2
Wartość wyrażenia jest równa
Przekształcamy podane wyrażenie:
Prawidłowa odpowiedź to odpowiedź A.
Zadanie 3
Kwotę zł wpłacamy do banku na lata. Kapitalizacja odsetek jest dokonywana w tym banku co kwartał, a roczna stopa oprocentowania wynosi . Po dwóch latach otrzymamy kwotę:
Skoro roczna stopa procentowa jest równa a kapitalizacja jest kwartalna, to znaczy, że stopa kwartalna jest równa
Jeżeli kwotę wpłacamy na okresów kapitalizacyjnych, a stopa procentowa za pojedynczy okres wynosi wówczas po okresach kapitalizacyjnych kwota na rachunku jest równa
W naszym przypadku oraz (dwa lata to osiem kwartałów). Wobec tego po dwóch latach otrzymamy kwotę
Prawidłowa odpowiedź to odpowiedź D.
Zadanie 4
Równość zachodzi dla
Mnożymy podaną równość stronami przez iloczyn mianowników, a następnie przekstałcamy:
Prawidłowa odpowiedź to odpowiedź B.
Zadanie 5
Układ równań
opisuje:
Metoda I
Przekształcamy podany układ równań:
Każde z równań ostatniego układu przedstawia prostą.
Współczynniki kierunkowe tych prostych są różne.
Zatem proste nie są równoległe, więc przecinają się w jednym punkcie.
Prawidłowa odpowiedź to odpowiedź B.
Metoda II
Rozwiązujemy podany układ równań:
Podstawiamy do pierwszego równania i rozwiązujemy otrzymane równanie z niewiadomą :
Podstawiamy w równaniu i wyznaczamy w ten sposób :
Tak więc układ ma jedno rozwiązanie Rozwiązanie to jest pojedynczym punktem
Prawidłowa odpowiedź to odpowiedź B.
Zadanie 6
Iloczyn wszystkich pierwiastków równania
jest równy:
Równanie jest spełnione wtedy i tylko wtedy, gdy przynajmniej jedno z wyrażeń w nawiasach jest równe zeru.
Mamy kolejno:
lub
Tak więc pierwiastkami równania są liczby
Iloczyn tych liczb jest równy
Prawidłowa odpowiedź to odpowiedź A.
Zadanie 7
Równanie ma dokładnie
Dziedziną równania jest zbiór tych liczb , które są różne od
Mnożymy równanie stronami przez , a następnie przekształcamy:
Dalszy ciąg rozwiązania możemy przeprowadzić dwiema metodami.
Metoda I
Zauważmy, że jednym z rozwiązań jest ponieważ obie strony równania są wtedy równe zeru.
Dla możemy równanie podzielić stronami przez i otrzymujemy:
Ostatecznie widzimy, że podane równanie ma dwa rozwiązania:
Prawidłowa odpowiedź to odpowiedź C.
Metoda II
Równanie możemy napisać jako
czyli
Rozwiązujemy otrzymane równanie kwadratowe.
Jego
wyróżnik
wyróżnik
jest równy
Mamy stąd
Rozwiązania
lub
naszego równania to
Prawidłowa odpowiedź to odpowiedź C.
Zadanie 8
Na rysunku przedstawiono wykres funkcji

Dziedziną funkcji jest
Odczytujemy dziedzinę z rysunku. Widzimy, że funkcja jest określona dla wszystkich spełniających warunek
Prawidłowa odpowiedź to odpowiedź C.
Zadanie 9
Na wykresie funkcji leży punkt zatem:
Punkt leży na wykresie funkcji wtedy i tylko wtedy, gdy
W naszym przypadku zatem musi zachodzić równość
Otrzymujemy stąd
Prawidłowa odpowiedź to odpowiedź B.
Zadanie 10
Funkcja liniowa ma takie samo miejsce zerowe, jak funkcja kwadratowa Wynika stąd, że
Zauważamy, że Wobec tego
Wynika stąd, że jedynym miejscem zerowym funkcji jest liczba
Ponieważ funkcja ma takie samo miejsce zerowe, jak funkcja , więc musi zachodzić równość
czyli
Otrzymujemy stąd
Prawidłowa odpowiedź to odpowiedź D.
Zadanie 11
Funkcja wykładnicza określona jest wzorem Jeżeli to
Ponieważ i , więc
Otrzymujemy stąd
Wzór naszej funkcji ma więc postać
Do podstawiamy wartosć i otrzymujemy
Prawidłowa odpowiedź to odpowiedź C.
Zadanie 12
Ile liczb całkowitych spełnia parę nierówności
?
Rozwiązujemy nierówność
Rozwiązujemy nierówność
Widzimy, że para nierówności jest spełniona dla
Do przedziału tego należą liczby Istnieje więc liczb spełniających podaną parę nierówności.
Prawidłowa odpowiedź to odpowiedź B.
Zadanie 13
W rosnącym ciągu geometrycznym spełniony jest warunek Iloraz tego ciągu jest równy
Na podstawie definicji ciągu geometrycznego możemy napisać
Mamy więc
Z drugiej strony w treści zadania podano, że zatem
Zachodzi więc równość
Ponieważ ciąg jest z założenia rosnący, więc jego iloraz musi być dodatni.
Zatem z równości otrzymujemy
Prawidłowa odpowiedź to odpowiedź B.
Zadanie 14
jest równy
Zachodzi równość
Korzystamy ze wzoru
Prawidłowa odpowiedź to odpowiedź B.
Zadanie 15
Jeżeli i to
Zachodzi równość
W treści zadania podano, że
Otrzymujemy więc
Prawidłowa odpowiedź to odpowiedź D.
Zadanie 16
Miara kąta środkowego jest o większa od miary kąta wpisanego opartego na tym samym łuku. Wynika stąd, że kąt środkowy ma miarę
Pamiętamy, że kąt środkowy ma miarę dwa razy większą od miary kąta wpisanego opartego na tym samym łuku.
Oznaczmy przez miarę kąta wpisanego. Wtedy miara kąta środkowego jest równa
Jednocześnie podano, że miara naszego kąta środkowego jest o większa od miary kąta wpisanego.
Zatem zachodzi równość
Tak więc miara kąta wpisanego jest równa
Szukana miara kąta środkowego jest dwa razy większa i równa
Prawidłowa odpowiedź to odpowiedź C.
Zadanie 17
Pole rombu o obwodzie cm jest równe cm Kąt ostry rombu ma miarę:
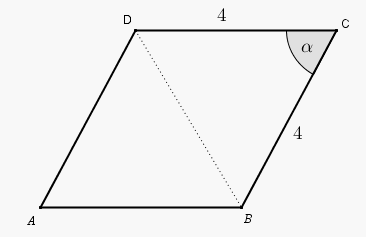
Nasz romb składa się z dwóch przystających trójkątów i Jego pole powierzchni jest więc dwa razy większe niż pole powierzchni każdego z tych trójkątów:
(korzystamy ze wzoru na pole trójkąta o bokach i kącie między nimi )
W treści zadania podano, że obwód rombu jest równy zatem długość każdego boku jest równa Mamy więc
W treści zadania podano, że Otrzymujemy więc
Prawidłowa odpowiedź to odpowiedź B.
Zadanie 18
Prosta jest równoległa do prostej wtedy i tylko wtedy, gdy
Dwie proste są
równoległe
wtedy i tylko wtedy, gdy mają takie same współczynniki
kierunkowe.
Współczynnik kierunkowy prostej jest równy
Współczynnik kierunkowy prostej jest równy
Proste i są więc równoległe wtedy i tylko wtedy, gdy
Stąd i ze wzoru skróconego mnożenia otrzymujemy
Prawidłowa odpowiedź to odpowiedź B.
Zadanie 19
Prosta jest prostopadła do prostej wtedy i tylko wtedy, gdy
Dwie proste są
Skorzystamy z
prostopadłe
wtedy i tylko wtedy, gdy iloczyn ich współczynników
kierunkowych jest równy
Współczynnik kierunkowy prostej jest równy
Współczynnik kierunkowy prostej jest równy
Proste i są więc prostopadłe wtedy i tylko wtedy, gdy zachodzi równość
Stąd i ze wzoru skróconego mnożenia otrzymujemy
Prawidłowa odpowiedź to odpowiedź B.
Zadanie 20
Dane są punkty i Punkt jest środkiem odcinka . Obrazem punktu w symetrii osiowej względem osi jest punkt
Rysunek poniżej ilustruje całą sytuację.
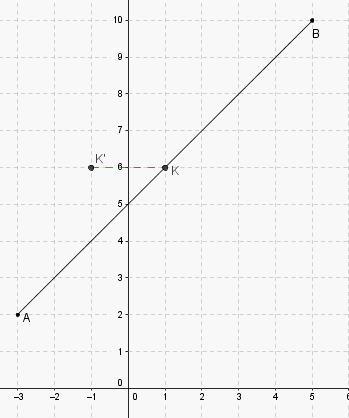
Rozumowanie algebraiczne wygląda natomiast tak.
Współrzędne punktu jako środka odcinka są średnimi arytmetycznymi odpowiednich współrzędnych punktów i
Zatem
Pamiętamy, że obrazem punktu w symetrii osiowej względem osi jest punkt (zmienia się znak współrzędnej ).
Wobec tego obrazem punktu w tej symetrii jest punkt
Prawidłowa odpowiedź to odpowiedź A.
Zadanie 21
Przekątna sześcianu o objętości cm ma długość
Oznaczmy długość krawędzi sześcianu przez .
Wtedy objętość sześcianu jest równa
W treści zadania podano, że objętość ta jest równa cm
Wobec tego
Długość krawędzi sześcianu (w cm) jest więc równa
Mamy wyznaczyć dlugość przekątnej sześcianu (czerwony odcinek na rysunku poniżej).
Korzystamy z twierdzenia Pitagorasa. Przy oznaczeniach jak na rysunku możemy napisać
Długość odcinka to (wyznaczone wcześniej).
Ponieważ (również na mocy twierdzenia Pitagorasa) więc
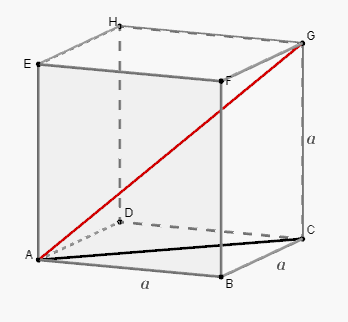
Tak więc długość przekątnej (w cm) jest równa
Prawidłowa odpowiedź to odpowiedź C.
Zadanie 22
W ostrosłupie prawidłowym trójkątnym krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem Długość krawędzi bocznej bryły jest równa cm. Jaka jest wysokość tego ostrosłupa ?
Przy oznaczeniach jak na rysunku dane są:
Mamy wyznaczyć
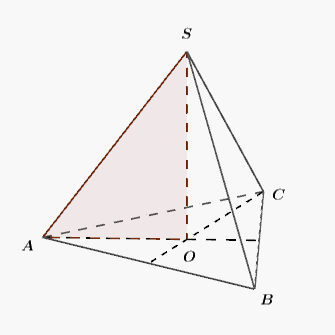
Możemy napisać
skąd
Ponieważ oraz więc mamy kolejno:
Prawidłowa odpowiedź to odpowiedź A.
Zadanie 23
Każda krawędź graniastosłupa prawidłowego trójkątnego ma długość równą Pole powierzchni całkowitej tego graniastosłupa jest równe
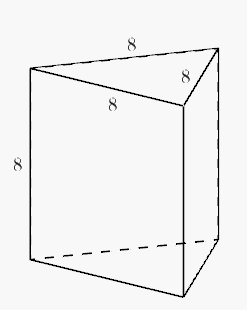
Podstawy naszego graniastosłupa są trójkątami równobocznymi. Każdy z tych trójkątów ma bok o długości
Wobec tego łączne pole powierzchni tych podstaw jest równe
Nasz graniastosłup ma ściany boczne będące kwadratami. Każdy z tych kwadratów ma bok o długości
Wobec tego pole powierzchni bocznej graniastosłupa jest równe
Zatem pole powierzchni całkowitej bryły jest równe
Prawidłowa odpowiedź to odpowiedź D.
Zadanie 24
Ustal średnią ważoną ocen Basi, przedstawionych wraz z wagami w tabelce poniżej:
| Ocena | 4 | 3 | 5 | 2 |
| Waga | 3 | 2 | 3 | 2 |
Obliczamy średnią ważoną według wzoru
gdzie to wartości w zbiorze danych, a – odpowiadające im wagi.
W naszym przypadku średnia ta wynosi
Prawidłowa odpowiedź to odpowiedź B.
Zadanie 25
Rzucamy dwa razy kostką sześcienną. Jakie jest prawdopodobieństwo, że iloczyn wyrzuconych oczek jest liczbą nieparzystą?
Za przestrzeń zdarzeń elementarnych przyjmijmy zbiór wszystkich uporządkowanych par liczb gdzie Liczba oznacza liczbę oczek po pierwszym rzucie, liczba oznacza liczbę oczek po drugim rzucie. Istnieje wszystkich takich par.
Zatem
Oznaczmy przez zdarzenie polegające na tym, że iloczyn wyrzuconych oczek jest liczbą nieparzystą.
Iloczyn dwóch liczb jest liczbą nieparzystą wtedy i tylko wtedy, oba czynniki są nieparzyste.
Zatem zdarzeniu sprzyjają wszystkie takie zdarzenia elementarne że zarówno jak jest liczbą nieparzystą:
Widzimy, że zdarzeniu sprzyja zdarzeń elementarnych, .
Zgodnie z definicją prawodpodobieństwa otrzymujemy:
Prawidłowa odpowiedź to odpowiedź C.
Zadanie 26
Rozwiąż nierówność
Przekształcamy podaną nierowność:
Aby uprościć dalsze obliczenia, mnożymy ostatnią nierówność stronami przez zmieniając przy tym jej kierunek i otrzymujemy
Wyznaczamy miejsca zerowe trójmianu
Jego
wyróżnik
wyróżnik
jest równy
Otrzymany wyróżnik jest dodatni, więc nasz trójmian ma dwa
miejsca zerowe:
lub
Znając miejsca zerowe, możemy zapisać trójmian w postaci iloczynowej
Nierówność przyjmuje więc postać
Szkicujemy wykres lewej strony nierówności:
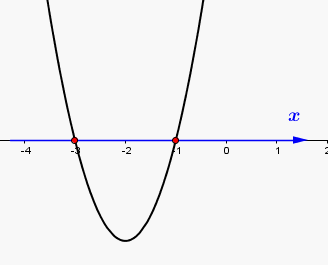
Odczytujemy z rysunku, że nierówność jest spełniona wtedy i tylko wtedy, gdy lub
Rozwiązaniem nierówności jest zbiór
Zadanie 27
Wykaż, że suma kwadratów dwóch kolejnych liczb nieparzystych przy dzieleniu przez daje resztę
Każdą liczbę nieparzystą możemy zapisać w postaci gdzie
Liczba nieparzysta występująca po liczbie to liczba o większa, czyli
Suma kwadratów liczby i liczby jest równa:
Widzimy więc, że suma kwadratów dwóch kolejnych liczb nieparzystych da się zapisać w postaci gdzie jest liczbą całkowitą (w naszym przypadku
Każda liczba postaci daje przy dzieleniu przez resztę
W ten sposób wykazaliśmy fakt będący treścią zadania.
Zadanie 28
Wykaż, że liczba jest podzielna przez
Liczba jest podzielna przez wtedy i tylko wtedy, gdy może być zapisana w postaci
gdzie jest liczbą całkowitą. Wykażemy, że podana w treści zadania liczba da się zapisać w takiej postaci.
W wyrażeniu wyłączamy przed nawias i otrzymujemy:
Przedstawiliśmy podaną liczbę w postaci (w tym przypadku ).
W ten sposób wykazaliśmy fakt będący treścią zadania.
Zadanie 29
Oblicz najmniejszą i największą wartość funkcji w przedziale
Wartość najmniejsza:
Wartość największa:
Współczynnik przy jest dodatni. Wobec tego wykresem funkcji jest parabola o ramionach zwróconych ku górze.
Wynika stąd, że nasza funkcja przyjmuje swoją najmniejszą wartość:
albo w punkcie będącym odciętą wierzchołka paraboli (jeżeli wierzchołek leży w podanym przedziale),
albo w którymś końcu podanego przedziału (jeżeli wierzchołek leży poza podanym przedziałem).
Odcięta wierzchołka wykresu funkcji jest równa
W naszym przypadku
Liczba ta leży wewnątrz przedziału zatem jest najmniejszą wartością naszej funkcji w całym przedziale. Wartość ta jest równa
Na końcach przedziału funkcja przyjmuje wartości:
Ostatecznie wnioskujemy, że:
– najmniejszą wartością funkcji w podanym przedziale jest
– największą wartością funkcji w podanym przedziale jest
Zadanie 30
Wyznacz równanie symetralnej odcinka , jeżeli oraz
Metoda I (algebraiczna)
Symetralna odcinka to prosta prostopadła do tego odcinka i przechodząca przez jego środek.
Środek naszego odcinka to punkt, którego współrzędne są średnimi arytmetycznymi odpowiednich współrzędnych punktów i
Musimy więc wyznaczyć równanie prostej przechodzącej przez punkt i prostopadłej do prostej przechodzącej przez punkty
Piszemy równanie prostej
Prosta prostopadła do prostej
ma współczynnik kierunkowy równy
(
dlaczego
)?
Zatem równanie szukanej prostej ma postać
Wartość wyznaczymy, wiedząc, że punkt należy do szukanej prostej.
Ostatecznie widzimy, że równanie szukanej prostej to
Metoda II (graficzna)
Rysujemy w układzie współrzędnych prostą zawierającą odcinek a następnie symetralną tego odcinka.
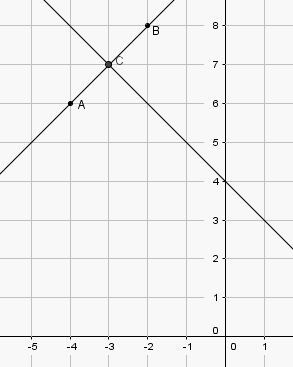
Widzimy z rysunku, że symetralna odcinka ma współczynnik kierunkowy równy ponieważ w przypadku tej prostej wzrost wartości o powoduje zmniejszenie wartości o
Ponadto symetralna przecina oś w punkcie Zatem w jej równaniu współczynnik musi być równy .
Ostatecznie widzimy, że równanie symetralnej to
Zadanie 31
Jeżeli licznik i mianownik pewnego ułamka nieskracalnego zwiększymy o , to otrzymamy Jeżeli zaś licznik tego ułamka powiększymy dwa razy, to otrzymamy Jaki to ułamek?
Zapiszmy ułamek w postaci
Z treści zadania odczytujemy, że
Przekształcając każdą z powyższych równości, otrzymujemy następujący układ równań:
czyli, po uproszczeniu drugiego równania,
Odejmując teraz pierwsze równanie od drugiego stronami, otrzymujemy
Podstawiając teraz do równania otrzymujemy
Ostatecznie otrzymujemy
Zatem szukany ułamek to
Zadanie 32
Podstawą ostrosłupa jest trójkąt . Krawędź jest wysokością ostrosłupa, jak na rysunku poniżej. Oblicz objętość tego ostrosłupa, jeżeli wiadomo, że oraz (wszystkie podane długości są w centymetrach).
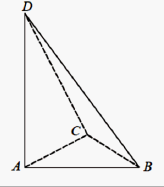
Rysunek poniżej przdstawia nasz ostrosłup z wymiarami podanymi w treści zadania.
Ponieważ więc ściana boczna jest trójkątem równoramiennym.
Krawędź jest wysokością bryły, zatem podstawa też jest trójkątem równoramiennym.
Objętość ostrosłupa jest równa
Ponieważ znamy więc musimy wyznaczyć pole powierzchni podstawy, a więc trójkąta .
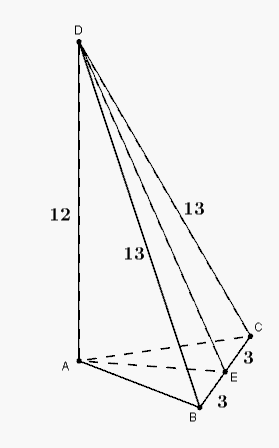
Bok tego trójkąta ma długość Musimy więc wyznaczyć długość jego wysokości.
Oznaczmy przez środek krawędzi . Ponieważ trójkąt jest równoramienny o ramionach i , więc odcinek jest jego wysokością, a to znaczy, że kąt (również kąt ) jest prosty. Wobec tego odcinek jest wysokością trójkąta .
Długość wysokości wyznaczymy z twierdzenia Pitagorasa dla trójkąta
czyli
W trójkącie kąt jest prosty (ponieważ jest wysokością bryły).
Stosując ponownie twierdzenie Pitagorasa, możemy napisać
Możemy teraz obliczyć pole powierzchni podstawy naszego ostrosłupa:
Ostatecznie objętość ostrosłupa jest równa
Zadanie 33
W pierwszej loterii jest losów, w tym losy wygrywające. W drugiej loterii jest losów, w tym losów wygrywających. Oblicz , wiedząc, że prawdopodobieństwo wygranej przy kupnie pojedynczego losu jest w pierwszej loterii trzykrotnie większe niż w drugiej.
Prawdopodobieństwo kupienia wygrywającego losu w pierwszej loterii. Z treści zadania wynika, że
Podobnie, prawdopodobieństwo kupienia wygrywającego losu w drugiej loterii jest równe
W treści zadania podano, że Otrzymujemy więc równanie z niewiadomą
Przekształcamy je:
Zadanie 34
Państwo Kowalscy mają troje dzieci, których wiek w latach opisują liczby tworzące ciąg geometryczny. Dzieci mają w sumie lat, a najstarsze z nich jest dziewięciolatkiem. Obliczy, ile lat ma każde dziecko.
Dzieci są wieku lat (licząc w kolejności od najmłodszego).
Skorzystamy z definicji ciągu geometrycznego.
Ponieważ
,
więc
.
Oznaczmy przez iloraz ciągu geometrycznego, który stanowią liczby opisujące wiek dzieci.
Z treści zadania odczytujemy, że najstarsze dziecko ma lat.
Wobec tego średnie dziecko ma lat.
Najmłodsze dziecko ma zatem (dlaczego?) lat.
Suma lat wszystkich dzieci jest równa . Możemy więc napisać:
Przekształcamy otrzymane równanie:
Rozwiązujemy otrzymane równanie kwadratowe z niewiadomą
Wyróżnik
wyróżnik
trójmianu
jest równy:
Wyróżnik jest dodatni oraz .
Równanie
ma dwa
rozwiązania:
lub
Rozwiązanie odrzucamy, ponieważ rozpatrywany ciąg jest rosnący (wiek dzieci podany jest w kolejności od najmłodszego do najstarszego).
Pozostaje rozwiązanie . Jest to iloraz naszego ciągu.
Ostatecznie liczby opisujące wiek dzieci w latach są następujące:
wiek najmłodszego dziecka to lata;
wiek średniego dziecka to lat;
wiek najstarszego dziecka (podany w treści zadania) to lat.